Mock Set 1 Paper 01 Non Calculator
Edexcel – foundation
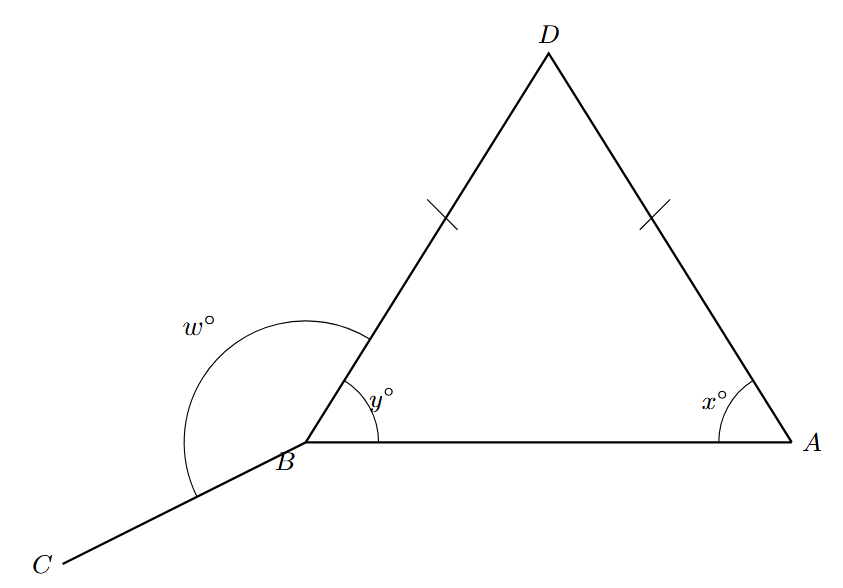
Question 23:
[Ad Space]
\[ \begin{aligned} &\text{The diagram shows an isosceles triangle } ABD \text{ and the straight line } DBC. \\ &AB = AD,\; x:y = 3:1. \\ &\text{Work out the value of } w. \end{aligned} \]