Higher Paper 2
Edexcel – higher
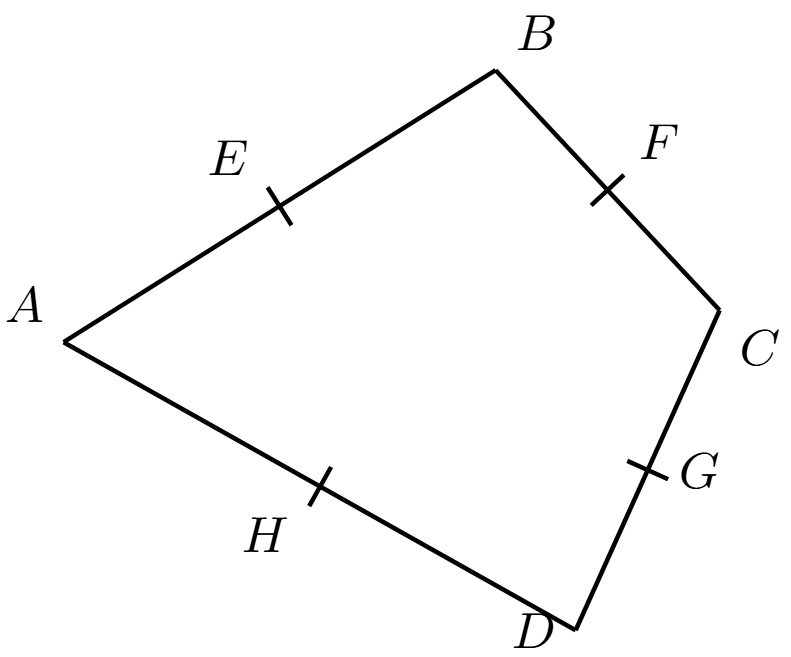
Question 18:
[Ad Space]
\begin{aligned} &\textit{ABCD} \text{ is a quadrilateral. } E,F,G,H \text{ are the midpoints of } AB,BC,CD,DA.\\[2mm] &\text{Prove, using vectors, that } EFGH \text{ is a parallelogram.} \end{aligned}